4.3 Lambert Reflektierer

Es wird eine punktförmige Lichtquelle angenommen, deren Licht gleichmäßig von der Oberfläche eines Objektes in alle Richtungen reflektiert wird, wie es in Abbildung 1 zu sehen ist.

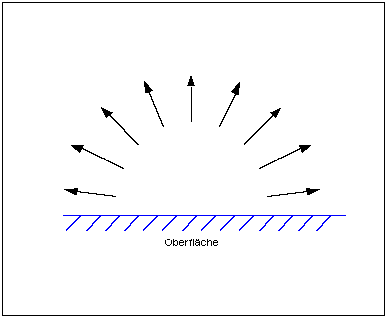
Abbildung 1

Zur Berechnung wird das Kosinusgesetz von Lambert verwendet, welches diesem Verfahren den Namen gegeben hat. Die Lichtintensität in einem Punkt der Körperoberfläche ist proportional zum Kosinus des Winkels 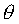zwischen Oberflächennormale N und dem Vektor L zur Lichtquelle.

Die Intensität ist also dann größer 0, wenn der Einfallswinkel 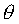zwischen 0° und 90° liegt. Bei negativem Winkel liegt die Lichtquelle hinter dem Objekt. Die Formel des lambertschen Gesetzes sieht folgendermaßen aus

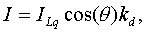
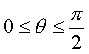
Die Konstante k_d ist der diffuse Reflexionskoeffizient der Oberfläche. k_d ist material- und wellenlängenabhängig und liegt im Wertebereich 0 <= k_d <= 1. Eine so berechnete Oberfläche würde matt erscheinen. Die Formel kann vereinfacht werden, wenn N und L als normierte Vektoren vorliegen, so dass der Kosinus als Skalarprodukt dargestellt werden kann. Daraus ergibt sich die Formel

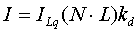
bzw.

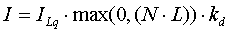
für beliebige Einfallswinkel.
Da hier, wie im Abschnitt über Ambientes Licht beschrieben, nur die direkt beleuchteten Flächen zu sehen wären, wird eine Hintergrundbeleuchtung hinzugefügt, was zu folgendem Modell führt

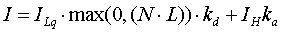
Die Konstante k_a ist der material- und wellenlängenabhängige ambiente Reflexionskoeffizient, 0 <= k_a <=1. In der Realität erscheinen zwei verschieden weit entfernte Objekte unterschiedlich hell, wogegen bei unserem bisherigen Modell diese Objekte mit der selben Intensität dargestellt werden. Aus der Praxis ist bekannt, dass die Helligkeit eines Körpers mit dem Quadrat der Entfernung d abnimmt. Der Ausdruck 1/d² liefert bei nahe dem Projektionszentrum liegenden Objekten zu starke Intensitätsunterschiede, so dass man lieber eine lineare Intensitätsreduktion mit dem Faktor 1/(d+d₀) verwendet. Der Wert d₀ ist eine beliebige Konstante, durch die eine Division durch Null bzw. eine Wertebereichsunterschreitung bei sehr kleinen Werten für f vermieden wird. Das resultierende Modell lautet

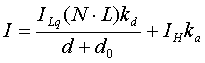
oder verallgemeinert für die Abstandsfunktion f(d)

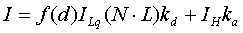
Für die verschiedenen Primärfarben des verwendeten Farbmodells müssen die Intensitäten einzeln berechnet werden, da diese verschieden von den Materialien absorbiert werden. Bei dem RGB-Modell ergibt sich folgendes Gleichungssystem

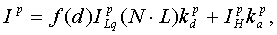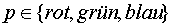
Dieses Modell beachtet nur die dominanten Wellenlängen, führt aber zu schon brauchbaren Resultaten.